Derivative of cos^-1(x)

Introduction

This article will explore a straightforward method for memorizing the derivative of cos^-1(x). We'll begin by outlining a simple three-step process that connects the derivative of cos(x) to cos^-1(x). Subsequently, we'll delve into the underlying reasons that contribute to the effectiveness of this process.

The process comprises three steps to derive inverse trigonometric derivatives from standard trigonometric derivatives:

1. Replace x with \(\theta\):

This step is crucial because, traditionally, x is regarded as the independent variable. In the context of "Derivative of cos(x)", the angle serves as the independent variable, and it is denoted as x. However, in inverse trigonometric derivatives, the functions themselves are treated as independent variables, while the angles become dependent variables. To align with this terminology, x is substituted with \(\theta\).

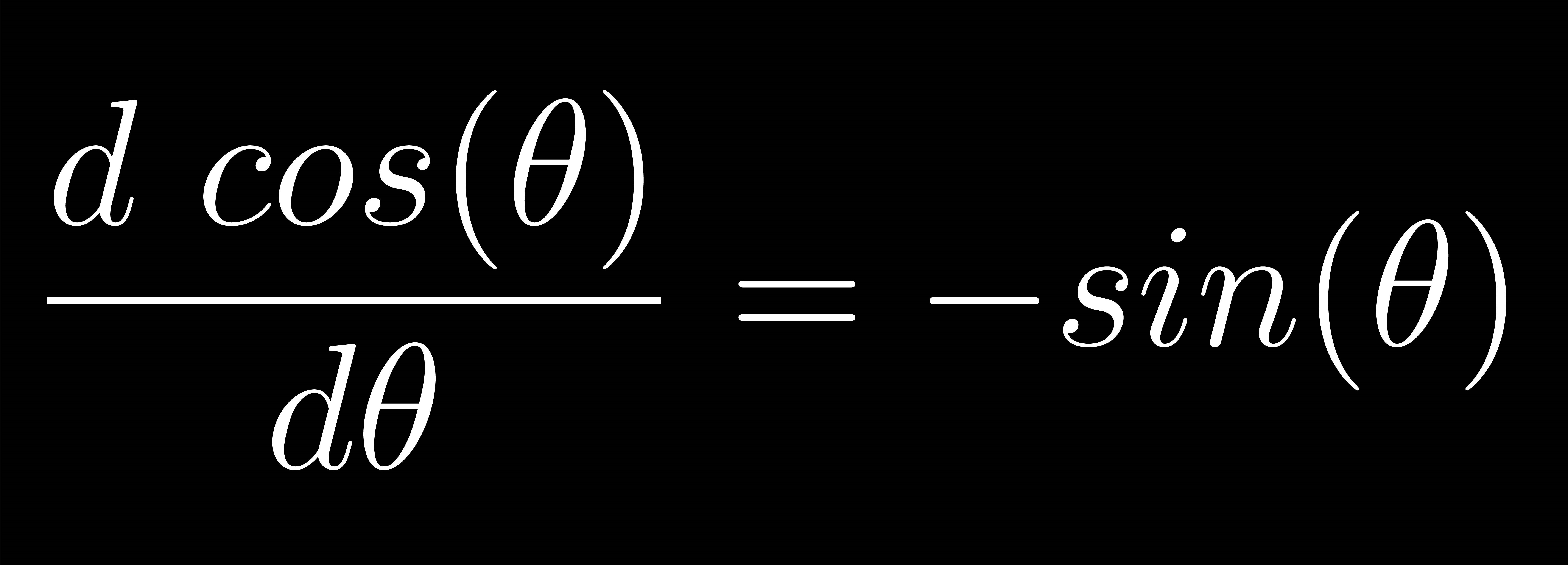
2. Substitute \(\theta\)-terms with x-terms:

Given that x is the independent variable, it is essential to express all the terms in the equation in relation to x. This ensures consistency with x being the independent variable in the context of inverse trigonometric derivatives.

3. Reciprocal of the numerator and denominator on both sides:

This marks the final step in transforming standard trigonometric derivatives into inverse trigonometric derivatives. It is noteworthy that the magnitude of the derivative is essentially the reciprocal of the standard trigonometric derivative. This observation stems from the fact that the preceding two steps involve only a change in the independent variable and a rewrite of terms in relation to that variable, maintaining the equality of the left-hand side (LHS) and right-hand side (RHS) values.